【アルゴリズムを学ぼう】#7 基本的なプログラムを作ってみる 6

　増井 敏克著「Pythonではじめるアルゴリズム入門 伝統的なアルゴリズムで学ぶ定石と計算量」で勉強しています。

2.6 フィボナッチ数列を作る

　ここでは、関数の中から自身の関数を呼び出す「再帰」を学びます。また、処理をたくさん繰り返す場合は処理が遅くなるので辞書を使って効率化する方法を学びます。

○フィボナッチ数列とは

　フィボナッチ数列というのは、直前の2つの項を足し合わせてできる数列のことで「1, 1, 2, 3, 5, 8, 13, 21, …」と無限に続いていきます。

　フィボナッチ数列の特徴としては、下図のように正方形を小さい方から２つ並べたものを１辺とする正方形を並べて長方形にする作業を繰り返すと、出来上がる長方形の縦と横の長さがフィボナッチ数列になります。

○再帰とは

　フィボナッチ数列を計算するプログラムを再帰を使って作っていきますが、再帰をしたときの動きを理解するために、足し算をするプログラムを再帰を使って作ってみます。

def sum(n):
    if n < 1: # ｎが1より小さくなったらn(=0)を返して終了
        print("0になるはず：　" + str(n))
        return n
    print(n)
    return n + sum(n-1) #左のｎは５、その後のsum(n-1) は４＋３＋２＋１を計算する
print("答え：　" + str(sum(5)))

　実行結果

5
4
3
2
1
0になるはず：　0
答え：　15

○再帰を使ったフィボナッチ数列を求めるプログラム

　続いて、フィボナッチ数列のn項目の値を求めるプログラムは以下のとおりです。

　ここでは、fibonacci関数に7を渡すと「13」という結果になります。

　「1,1,2,3,5,8,13,・・・」。「13」は7項目にありますね。

def fibonacci(n):
    if (n == 1) or (n == 2): #終了条件
        return 1
    return fibonacci(n - 2) + fibonacci(n - 1) #計算式   
print(fibonacci(7))

　実行すると「13」になります。

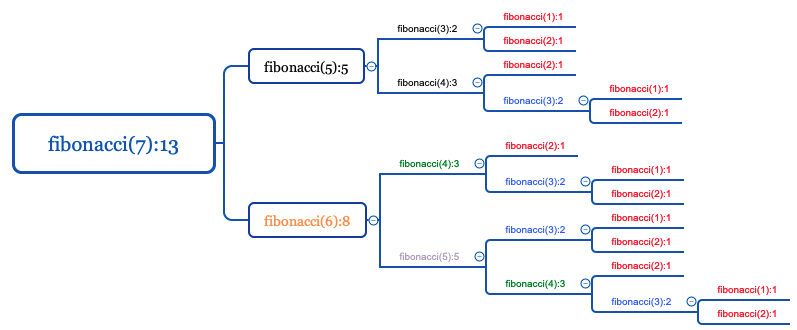
　fibonacci関数に最初に7を渡した後、上述のプログラムのコメントの「#計算式」のところではどのように再帰的に計算をしているかというと、下図のようにfibonacci(n - 2)はfibonacci(５)、fibonacci(n - 1)はfibonacci(6)と２手に分かれて、更にどんどん奥深く降りていき、最終的には下図の赤字のように終了条件となる「1」か｢2｣が出てきたら戻り値として１を返してそれを足し上げるという処理をしています。赤字は13個あります。

　GoogleのColaboratoryで「fibonacci(35)」で計算すると約３秒、「fibonacci(40)」にして動かすと約33秒かかり、数を増やせばどんどん計算に時間がかかっていきます。なぜかというと、上図を見ると例えば「fibonacci(3)」は５回も同じ計算がされており、数を増やせば同じ計算をしている箇所がどんどん増えていくからです。

　なので、この繰り返し同じ計算をしているところをメモ化して、計算時間を短くしていきます。

○メモ化によって処理を高速化する

memo = {1:1, 2:1} #辞書に終了条件の値を入れる
def fibonacci(n):
    if n in memo:
        return memo[n] #辞書に登録されていれば、その値を返す
    memo[n] = fibonacci(n - 2) + fibonacci(n - 1) #辞書に登録がなければ計算して辞書に登録する
    return memo[n]
fibonacci(7)

　実行すると「13」になります。

　１つ前のプログラムでは、fibonacci(40)」にして動かすと約33秒かかりましたが、こちらでは１秒もかからず計算が終了しました。

　こちらのプログラムではまず最初にmemoという辞書に終了条件の値を入れています。Pythonのデータ型のディクショナリは {キー1:値1,キー2:値2,・・・}というキーと値の組み合わせで構成されます。つまりmemoにはフィボナッチ数列の最初の２つの「1」を辞書に入れているということになります。

　最初のif文では、memoの中に既に計算あるいは初期値として設定されたキーがあるかないかを調べていきます。したがって最初にfibonacci関数に「7」を渡すと、if文の箇所でmemoに「7」というキーがあるか調べます。「7」はまだ無いので、再帰処理の方に進みます。

　再帰処理では、 fibonacci(n - 2) つまりfibonacci関数に「5」を渡すことになります。次のif文の箇所でもまだ「5」は無いので更に繰り返し辞書があるところまで降りていきます。下図でいうと最上部右のfibonacci(1)とfibonacci(2)まで行くと、初期に設定したキー１、２が見つかるので、if文の戻り値として、それぞれのキーに対応する値が返されます（それぞれ「1」となる）。つまり、最初にmemo[n] = fibonacci(n - 2) + fibonacci(n - 1) が計算されるのは「n」が「3」のときで、 fibonacci(n - 2) は「1」、 fibonacci(n - 1) も辞書から「1」が呼び出され、memoに新たなキー「3」として1+1の合計である値「2」が辞書に登録されます。memo = {1: 1, 2: 1, 3: 2}となります。一度登録されると下図の青字の箇所のfibonacci(3)の計算はしないで済むようになります。同じように緑のfibonacci(4)も2回余分な計算をしないで済むようになります。

　このような手法は「メモ化」と呼ばれパズルなどの問題を解くときに使われたりするそうです。

　以上の他にループによりフィボナッチ数列を求めるプログラムも掲載されていますので、参考に載せておきます。

def fibonacci(n):
    fib = [1,1]
    for i in range(2, n):
        fib.append(fib[i-2] + fib[i-1])
    return fib[n - 1]
fibonacci(7)